표준 모형
소립자 물리학의 표준 모형(標準模型, 영어: Standard Model)은 자연계의 기본 입자와, 중력을 제외한 그 상호작용
(강한 상호작용, 약한 상호작용, 전자기 상호작용)을 다루는 게이지 이론이다.
강력을 다루는 양자 색역학과, 약력과 전자기력을 다루는 와인버그-살람 이론으로 이루어진다.
표준 모형에 따르면, 전자와 중성미자 및 기타 렙톤은 기본 입자이나, 강입자는 쿼크로 이루어진다.
이들은 게이지 보손에 의하여 상호작용한다.
게이지 보손은 이론의 대칭을 나타낸다.
표준 모형의 대칭 가운데 강한 상호작용의 대칭은 가둠으로 인하여 간접적으로만 관찰할 수 있고,
약한 상호작용의 대칭은 힉스 메커니즘으로 인하여 깨진다.
따라서 거시적으로는 전자기 상호작용의 대칭만 쉽게 관찰할 수 있다.
표준 모형은 실험적으로 힉스 메커니즘을 제외하고 1980년대에 완성되었다.
힉스 메커니즘은 2010년대 초에 실험적인 증거가 발견되었다.
표준 모형의 페르미온[편집]
표준 모형에서는 중성미자와 게이지 보손, 힉스 보손을 제외한 모든 입자를 디랙 입자로 나타낸다.
이들 입자는 스핀 ½(즉 페르미온)을 가지며, 질량과 전하를 가지고, 그 반입자와 서로 다르다.
표준모형은 이들 입자의 질량을 예측하지 못하나, 대체로 세대가 높을 수록 더 무겁다.
표준 모형의 디랙 입자 중, 강하게 상호작용하는 입자는 쿼크, 그렇지 않는 입자는 중성미자와 함께 렙톤으로 분류한다.
쿼크는 ±⅓ 혹은 ±⅔의 전하를 가지고, 중성미자가 아닌 렙톤은 ±1의 전하를 가진다.
이들 입자는 힉스 메커니즘으로 질량을 얻는다. 중성미자는 바일 입자(손지기 페르미온)으로 나타낸다.
즉 스핀 ½(즉 페르미온)을 가지며, 질량과 전하가 없고, 그 반입자와 다른 손지기(chirality)를 가진다.[1]
6종의 쿼크 맛깔은 시간이 지나면서 서로 다른 맛깔의 쿼크로 변할 수 있는데,[2] 이를 쿼크 섞임이라고 한다.
쿼크가 섞이는 정도는 CKM행렬이라는 수학적 개체로 나타낸다.
이는 이탈리아의 니콜라 카비보(Nicola Cabbibo)와 일본의 고바야시 마코토와 마스카와 도시히데가 도입하였다.
예를 들어, 중성자는 양성자로 붕괴할 수 있다 (베타 붕괴).
쿼크 섞임 때문에 표준 모형은 CP 대칭을 보존하지 않는다.
렙톤의 경우, 표준 모형에서는 렙톤이 섞이지 않는다.
즉, 표준모형은 세 종류의 렙톤 수 (전자 수, 뮤온 수, 타우온 수)를 개별적으로 보존한다.[3]
표준모형의 페르미온은 다음과 같이 세 세대로 나뉜다.
각 세대의 서로 대응되는 입자는 질량을 제외하고는 정확히 같은 성질을 지닌다.
표준 모형은 왜 세대 구조가 존재하는지 설명하지 못한다.
| 이름 | 기호 | 전하 | 색 | 질량 | |
| 1세대 | |||||
| 전자 | e− | −1 | (없음) | 0.511 MeV | |
| 전자 중성미자 | νe | 0 | (없음) | 0[4] | |
| 위 쿼크 | u | +⅔ | 빨강/초록/파랑 | ~5 MeV | |
| 아래 쿼크 | d | −⅓ | 빨강/초록/파랑 | ~10 MeV | |
| 2세대 | |||||
| 뮤온 | μ− | −1 | (없음) | 105.6 MeV | |
| 뮤온 중성미자 | νμ | 0 | (없음) | 0[4] | |
| 맵시 쿼크 | c | +⅔ | 빨강/초록/파랑 | ~1.5 GeV | |
| 기묘 쿼크 | s | −⅓ | 빨강/초록/파랑 | ~100 MeV | |
| 3세대 | |||||
| 타우온 | τ− | −1 | (없음) | 1.784 GeV | |
| 타우온 중성미자 | ντ | 0 | (없음) | 0[4] | |
| 꼭대기 쿼크 | t | +⅔ | 빨강/초록/파랑 | 178 GeV | |
| 바닥 쿼크 | b | −⅓ | 빨강/초록/파랑 | ~4.7 GeV | |
표준 모형의 게이지 보손
표준 모형은 게이지군이 SU(3)C×SU(2)W×U(1)Y인 게이지 이론이다.
이 중 강력은 SU(3)C, 약전자기력은 SU(2)W×U(1)Y에 해당한다. 낮은 에너지에서, 약전자기력의 대칭은 힉스 메커니즘에
의해 자발적으로 깨져 전자기력의 U(1)EM만 남고, 나머지는 약력을 이룬다.
이 과정으로 인해 힉스 보손과 약력의 게이지 보손은 질량을 얻는다.
(여기서 U(1)Y와 U(1)EM은 서로 다른 군이다.)
강력의 게이지 보손은 글루온이다. SU(3)가 8차원이므로, 글루온은 총 여덟가지의 색을 지닌다.
강력은 오직 쿼크에만 작용하고, 렙톤에는 작용하지 않는다.
쿼크는 세가지의 색을 지닌다.[5] 이를 가시광선의 삼원색을 따서 통상적으로 빨강, 초록, 파랑으로 부른다.[6]
이 때문에 강한 상호작용을 기술하는 양자장론을 양자 색역학이라고 일컫는다.
글루온을 통하여 쿼크의 색이 바뀔 수 있다.
따라서 글루온의 색을 3가지의 색을 다른 색으로 바꾸는 조합 (초록→빨강, 빨강→파랑 등)으로 볼 수 있다.
3가지의 색을 다른 3가지로 바꾸는 조합은 총 3×3=9가지이나, 그중 모든 색을 그대로 두는
(빨강→빨강, 초록→초록, 파랑→파랑) 변환을 제외하여[7] 8가지의 색이 남는다.
전약력의 게이지 보손은 SU(2)×U(1)이 4차원이므로 4종인데, 이는 대칭 깨짐 이전의 W+, W-, W0 (약한 아이소스핀,
SU(2)), B (약한 초전하, U(1))에 해당한다.
대칭 깨짐 이후, W0과 B는 광자와 Z보손으로 섞인다.
전약력의 게이지 군 가운데 SU(2)의 전하는 약한 아이소스핀, U(1)의 전하는 약한 초전하이다.
대칭이 깨지면서, 약한 아이소스핀의 한 성분과 약한 초전하가 섞여 양자전기역학의 대칭군 U(1)을 이룬다.
| 상호작용 | 게이지 군 | 보손 | 기호 | 전하 | 질량 |
| 전자기력 | SU(2)×U(1) | 광자 | γ | 0 | 0 |
| 약한 상호작용 | Z보손 | Z0 | 0 | 91.19 GeV | |
| W보손 | W± | ±1 | 80.2 GeV | ||
| 강한 상호작용 | SU(3) | 글루온 | g | 0 | 0 |
표준 모형의 이론적 구성
대칭
표준 모형은 대부분의 양자장론처럼 많은 수의 대칭을 지닌다. 대칭은 다음과 같이 분류할 수 있다.
연속적 대칭: 이들을 리군을 이룬다. 연속적 대칭은 뇌터 정리에 의하여 해당하는 보존량을 가진다.
전반적 대칭: 모든 곳의 마당 전체를 변환하는 대칭.
우연한 대칭: 이론에서 가정하지 않았으나 "우연히" 생겨난 대칭. 비(非)건드림이론 차원에서 깨질 수 있다.
게이지 대칭 (국소적 대칭): 특정한 구역의 마당만 변환하는 대칭. 이런 대칭을 가진 이론을 게이지 이론이라고 한다.
이산대칭
자연계에서 약력은 C 대칭과 P 대칭을 최대로 깬다.
따라서 표준 모형은 이들을 따르지 않는다.
강력의 경우 이론적으로 C 대칭을 깰 수 있으나 (강력 CP 문제), 이는 관측 불가능할 정도로 작다.
약력은 2세대 이하에서는 CP 대칭을 보존하지만 3세대 이상으로는 CP 대칭을 깬다 (CP 위반).
표준 모형은 다른 모든 특수상대론적 이론과 같이 푸앵카레 대칭을 따르므로 CPT 정리에 따라 CPT 대칭을 따른다.
CPT는 이산대칭이기 때문에 뇌터 정리에 해당하지 않고,연관된 보존량도 없다.
게이지 대칭
표준 모형은 SU(3)×SU(2)×U(1)의 대칭군을 가진 게이지 이론이다.
여기서 SU(3)은 색력에 해당하고, SU(2)×U(1)은 전약력에 해당한다.
SU(2)를 약한 아이소스핀, U(1)을 약한 초전하라고 부른다.
이 중 SU(2)×U(1)은 U(1)으로 깨지게 된다.
여기서 깨진 후 남은 U(1)은 전자기 대칭으로, 약한 초전하의 U(1)과는 다르다.
이에 따라 표준 모형은 색전하, 약한 아이소스핀, 약한 초전하를 보존한다.
우연한 대칭
표준 모형은 건드림이론 수준에서 네 가지의 전반적 (global) 우연대칭 (accidental symmetry)을 가진다.
이는 쿼크 위상 회전, 전자 위상 회전, 뮤온 위상 회전, 타우온 위상 회전이다.
이에 따라, 표준 모형은 바리온 수, 전자 수, 뮤온 수, 타우온 수를 보존한다.
이들은 우연대칭이기 때문에, 대통일 이론에서 깨질 수 있다.
실제로 전자 수, 뮤온 수, 타우온 수의 개별적인 보존은 중성미자 진동에 의하여 반증되었다.
또한, 우연대칭은 건드림이론에서는 성립하지만 비(非)건드림적인 효과로 인해 깨질 수 있다.
실제로 표준 모형에서는 비건드림적 효과로 인하여 바리온 수와 렙톤 수가 개별적으로 보존되지 않는다.
즉 B+L은 보존되지 않을 수 있다.
이를 스팔레론(sphaleron)이라고 부른다. 그러나 B−L은 비건드림적으로도 보존된다.
물론 모든 비건드림이론적 효과는 대부분의 경우 극히 미미하고, 빅뱅 초기 (바리온 생성 및 렙톤 생성)를 제외하고는
관측하기 힘들다.
이 밖에도, 표준 모형은 각종 근사적인 맛깔 대칭을 지닌다.
가장 기본적으로 아이소스핀의 SU(2)와 이를 초전하로 확장한 SU(3)이 있고,
이를 다른 쿼크를 도입하여 더 확장할 수 있다.
맛깔 대칭은 쿼크의 질량에 의하여 깨진다. 질량이 클 수록 깨지는 정도도 더 심하다.
| 대칭 | 리 군 | 종류 | 보존량 |
|---|---|---|---|
| 푸앵카레 | ISO(1,3) | 전반적 대칭 | 4차원 운동량 · 각운동량 |
| 색 | SU(3) | 게이지 대칭 | 색전하 |
| SU(2)L | SU(2) | 게이지 대칭 | 약한 아이소스핀 |
| U(1)Y | U(1) | 게이지 대칭 | 약한 초전하 |
| 쿼크 위상 | U(1) | 전반적 우연대칭 | 중입자수 |
| 전자 위상 | U(1) | 전반적 우연대칭 | 전자 수 |
| 뮤온 위상 | U(1) | 전반적 우연대칭 | 뮤온 수 |
| 타우온 위상 | U(1) | 전반적 우연대칭 | 타우온 수 |
| CPT | Z2 | 이산대칭 | (없음) |
장[편집]
아래의 표는 표준 모형에 등장하는 모든 마당을 정리한 것이다.
이 가운데 페르미온 장 (스핀 ½)은 질량을 제외하고 모든 성질이 같은 두 개의 세대가 더 존재하지만, 생략하였다.
이 표는 왼손 바일 스피너 대신에 오른손 바일 스피너로 적을 수도 있다.
그렇게 하면, 모든 쿼크를 반쿼크로 바꾸어야 한다.
이는 약력은 전반성 (P) 대칭을 최대로 불복하기 때문이다.
또한, 표준 모형에서 중성미자는 오직 왼손만 존재한다.
즉 모든 중성미자는 왼손잡이며, 반중성미자는 오른손잡이다.
페르미온의 경우, 왼손 입자( ,
,  )는 SU(2)L의 기본표현(fundamental representation)을 따르나, 왼손 반입자(
)는 SU(2)L의 기본표현(fundamental representation)을 따르나, 왼손 반입자( ,
,  ,
, 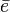 )
)
는 SU(2)L에 따라 변환하자 않는다. (반)쿼크( ,
,  ,
,  )는 SU(3)c의 (반)기본표현을 따르나, 렙톤(
)는 SU(3)c의 (반)기본표현을 따르나, 렙톤( ,
, 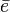 )은 SU(3)c에
)은 SU(3)c에
따라 변환하지 않는다.
게이지 장( ,
,  ,
,  )은 해당 게이지 대칭에 대하여 딸림표현을 따르고, 로렌츠 벡터이며, 다른 게이지 대칭에는
)은 해당 게이지 대칭에 대하여 딸림표현을 따르고, 로렌츠 벡터이며, 다른 게이지 대칭에는
변환하지 않는다.
| 장 (1세대) | 기호 | 로런츠 표현 | SU(3)c 표현 | SU(2)L 표현 | U(1)Y 표현 | 중입자수 | 렙톤 수 |
|---|---|---|---|---|---|---|---|
| 왼손 쿼크 |  |
(½,0) | 3 | 2 | ⅓ | ⅓ | 0 |
| 왼손 위 반쿼크 |  |
(½,0) | 3 | 1 | −1⅓ | −⅓ | 0 |
| 왼손 아래 반쿼크 |  |
(½,0) | 3 | 1 | ⅔ | −⅓ | 0 |
| 왼손 렙톤 |  |
(½,0) | 1 | 2 | −1 | 0 | 1 |
| 왼손 양전자 |  |
(½,0) | 1 | 1 | 2 | 0 | −1 |
| 약한 초전하 게이지 |  |
(½,½) | 1 | 1 | 0 | 0 | 0 |
| 약한 아이소스핀 게이지 |  |
(½,½) | 1 | 3 | 0 | 0 | 0 |
| 글루온 |  |
(½,½) | 8 | 1 | 0 | 0 | 0 |
| 힉스 보손 |  |
(0,0) | 1 | 2 | 1 | 0 | 0 |
상수[편집]
표준 모형은 19개의 상수를 포함한다.
| 기호 | 이름 | 재규격화방식 | 값 |
|---|---|---|---|
| me | 전자 질량 | 511 keV | |
| mμ | 뮤온 질량 | 106 MeV | |
| mτ | 타우온 질량 | 1.78 GeV | |
| mu | 위 쿼크 질량 | μMS = 2 GeV | 2.3 MeV |
| md | 아래 쿼크 질량 | μMS = 2 GeV | 4.8 MeV |
| ms | 기묘 쿼크 질량 | μMS = 2 GeV | 95 MeV |
| mc | 맵시 쿼크 질량 | μMS = mc | 1.275(25) GeV |
| mb | 바닥 쿼크 질량 | μMS = mb | 4.18(3) GeV |
| mt | 꼭대기 쿼크 질량 | 질량껍질 위 방식 | 173.07(±0.52±0.72) GeV |
| θ12 | 1세대-2세대 쿼크 섞임 각 | 13.1° | |
| θ23 | 2세대-3세대 쿼크 섞임 각 | 2.4° | |
| θ13 | 1세대-3세대 쿼크 섞임 각 | 0.2° | |
| δ | 쿼크 섞임 CP 위반 위상 | 0.995 | |
| g1 | 전약력 U(1)Y 결합상수 | μMS = mZ | 0.357 |
| g2 | 전약력 SU(2)L 결합상수 | μMS = mZ | 0.652 |
| g3 | 색력 결합상수 | μMS = mZ | 1.221 |
| θQCD | 색역학 CP 위반 진공각 | <10−10 | |
| v | 힉스 장 진공 기댓값 | 246 GeV | |
| mH | 힉스 보손 질량 | 125.9(4) GeV |
표준 모형의 결함
표준 모형은 이론적으로 여러가지의 결함을 가지고 있고, 또 현상론적으로 관측된 일부 현상을 설명하지 못한다.
이 때문에 학자들은 표준모형이 더 기본적인 이론을 근사하는 유효 이론이며, 더 높은 에너지에서는 표준모형이
다루지 않는 새 현상이 나타나리라고 기대한다
거대 하드론 충돌기에서 행해지는 여러 실험은 표준모형의 한계를 드러낼 것이다.
이론적 결함
표준 모형은 이론적으로 여러 자연스러움 (naturality) 문제를 안고 있다.
이는 표준 모형에 등장하는 몇몇 상수가 너무나 큰 값 또는 작은 값을 가지는 것이다.
이런 문제를 해결하려면 대개 더 강력한 대칭을 도입하여 상수가 왜 그렇게 크거나 작은 값을 가지는지 설명해야한다.
이런 종류의 이론은 대통일 이론이나 초대칭 따위가 있다.
- 계층 문제
- 전약력의 자발 대칭 깨짐이 일어나는 눈금은 플랑크 눈금보다 터무니없이 작다.
- 표준 모형에서는 전약력 대칭 파괴는 스칼라 힉스 보손으로 일으켜지나,
- 스칼라 입자의 질량은 (초대칭이 없는 이상) 방사 보정에 대하여 안정하지 못하다.
- 따라서 일반적으로 새로운 물리가 나타나는 눈금(대통일 눈금이나 플랑크 눈금) 정도이여야 하는데,
- 힉스 보손의 질량은 플랑크 질량보다 훨씬 작다.
- CP 위반 문제
- 강력이 CP대칭을 위반하는 정도는 지나치게 작다.
- 우주 상수 문제
- 진공의 에너지 밀도는 플랑크 에너지 밀도에 비하여 지나치게 작다.
- 이론적으로는 진공에너지(우주상수)는 무한대이거나 중력을 고려하면 플랑크 에너지 눈금에 있어야 하는데,
- 관측된 값은 이보다 훨씬 작다.
또한, 표준 모형은 여러가지로 임의적인 면이 있다.
표준 모형은 3세대로 구성되어 있지만, 왜 3세대로 구성되었는지 설명하지 않는다.
2세대가 발견되었을 때, 이지도어 아이작 라비는 "누가 그걸 주문했어?"라고 외칠 정도로, 세대의 존재와
그 수는 언뜻 보면 불필요한 구조다.
표준 모형은 전하의 양자화를 설명하지 않는다. 폴 디랙은 전하의 양자화를 설명하려면 자기 홀극이 필요하다는 사실을
보였으나 표준 모형은 자기 홀극을 포함하지 않는다.
또한 표준 모형은 19개의 자유 변수를 가진다. 이 자유 변수의 수는 기본 이론이라고 보기에는 너무 많다.
현상론적 결함
표준 모형은 입자 물리학의 거의 모든 실험 결과를 오차 범위 안으로 설명한다.
그러나 표준모형은 중력을 다루지 않는다.
또 표준 모형은 중성미자를 무질량 입자로 다루지만, 실제로 중성미자는 아주 작지만 영이 아닌 질량을 가진다
(중성미자 진동). 이 질량이 어떤 종류인지 (즉 중성미자가 디랙 입자인지 마요라나 입자인지) 아직 확실하지 않다.
또한 표준 모형은 아무런 암흑 물질 입자를 포함하지 않는다. 표준 모형에서 암흑 물질로 간주할 수 있는 입자는
중성미자밖에 없는데, 중성미자는 이론적으로 전체 암흑 물질 양의 소량만을 차지한다.
각주[편집]
1. 이동 ↑ 실제 중성미자는 미세하지만 질량을 가진다. 중성미자의 질량을 설명하려면 시소 메커니즘 따위가 필요하다.
2. 정확히 말하면, 쿼크의 질량 기저가 맛깔 기저와 다르다.)
3. 이동 ↑ 실제로, 렙톤 가운데 중성미자는 섞일 수 있다. 이를 중성미자 진동이라고 하며, 이 현상은 폰테코르보 마키
나카가와 사카타 (PMNS) 행렬에 의하여 나타낸다. 즉, 실제로 세 종류의 렙톤 수는 표준 모형과 달리 개별적으로
보존되지 않는다.
4. 이동: 가 나 다 표준 모형에서 중성미자의 질량은 정의할 수 없다.
5. 이동 ↑ 다시 말해, 강력의 SU(3)는 쿼크에 3중항 표현으로 작용한다.
6. 이동 ↑ 양자 색역학의 색은 이름 밖에는 가시광선의 색과 무관하다.
7. 이동 ↑ 즉, 리 대수 U(3)=SU(3)×U(1)에서 가환하는 U(1)을 제외하는 것.
