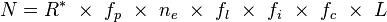드레이크 방정식(Drake equation)은 인간과 교신할 수 있는 지적인 외계 생명체의 수를 계산하는 방정식이다. 1960년대에 방정식을 최초로 고안한 프랭크 드레이크 박사의 이름이 붙었다. 그린 뱅크 방정식(Green Bank equation) 또는 세이건 방정식(Sagan equation)이라고도 한다.
드레이크 방정식은 페르미 역설과 밀접한 관련이 있다.
방정식
드레이크 방정식은 다음과 같다.
- N: 우리 은하 내에 존재하는 교신이 가능한 문명의 수
- R*: 우리은하 안에서 탄생하는 항성의 생성률 (= 우리은하 안의 별의 수/평균 별의 수명)
- fp: 이들 항성들이 행성을 갖고 있을 확률 (0에서 1 사이)
- ne: 항성에 속한 행성들 중에서 생명체가 살 수 있는 행성의 수
- fl: 조건을 갖춘 행성에서 실제로 생명체가 탄생할 확률 (0에서 1 사이)
- fi: 탄생한 생명체가 지적 문명체로 진화할 확률 (0에서 1 사이)
- fc: 지적 문명체가 다른 별에 자신의 존재를 알릴 수 있는 통신 기술을 갖고 있을 확률 (0에서 1 사이)
- L: 통신 기술을 갖고 있는 지적 문명체가 존속할 수 있는 기간 (단위: 년)
추정값
각각의 값에는 해답이 없기 때문에, 개인마다 상당히 다양한 값이 나왔다. 드레이크가 1961년에 사용한 값은 다음과 같다.
- R* = 10/년
- fp = 0.5
- ne = 2
- fl = 1
- fi = 0.01
- fc = 0.01
- L = 10,000 년
참고로, 이 방정식은 L의 값에 따라 달라지는데, 이 L값은 사람에게 달려있다고 한다.
※아레시보 메시지
지구인이 외계인과 교신하려는 시도 중의 하나는 1974년 푸에르토리코에 위치한 아레시보 천문대에서 은하계의 구상성단 M13에 마이크로파로 발사한 아레시보 메시지이다. 구상성단 M13과 같이 오래된 별을 택한 이유는 메시지를 해독할 정도의 지능을 갖추려면 생명체가 오랜 시간 동안 진화하는 과정이 필요해서다. 아레시보 메시지는 인류가 이룬 정신문명의 핵심이면서 지능을 가진 외계인이 이해할 수 있다고 생각하는 내용을 이진법으로 표현했다.
아레시보 메시지로 왜 이진법을 선택했을까? 우리가 현재 사용하는 십진법은 인간의 손가락이 10개라는 사실에서 비롯된 다분히 임의적인 선택이다. 예를 들어 어떤 행성에 손가락이 7개인 외계인이 산다면 그들은 칠진법을 당연시하며 사용할 수 있다. 이에 비해 이진법은 0과 1, 있음과 없음과 같이 상반된 상태를 나타내는 두 가지 기호로 이루어졌으므로 외계에서 혹시 다른 진법을 사용해도 이진법을 이해할 가능성이 높다.
삶이 무료해지거나 사소한 일상사에 마음을 쓰고 싶지 않을 때 이를 치유하는 방법 중의 하나는 우주와 같은 거시 세계에 대해 생각해 보는 것이다. 지구는 태양계에 속하고 태양계는 광대한 은하계의 극히 일부분이고 그런 은하계가 수도 없이 많다면 도대체 우주는 얼마나 넓을까? 그런 우주에 대해 경외감을 가져 보고, 많고 많은 별 중에 우리와 비슷한 지능을 가진 생명체가 하나쯤은 존재하지 않을까 생각하다 보면 현재 집착하고 있는 눈앞의 상황에서 어느 정도 초연해질 수 있다.